

We choose parameters c = 2% and k = 20%, which are commonly used in hedge fund compensation contracts. Also, we set the risk-free rate r = 5%, and the growth rate of the HWM g=r given that the fund's AUM always grows at least at the risk-free rate r. The rates are annualized. It can be seen that λ and δ have the same effect on value functions, since in Eqs. (13) and (16), they appear additively. Let λ = 10%, δ = 0, indicating that, just considering the probability of exogenous liquidation, the implied fund duration is on average ten years and investors do not receive withdrawals from the fund. It is equivalent to letting δ = 10%, λ = 0, reflecting that investors receive continuous withdrawals at the rate 10% with no exogenous liquidation. According to Lan et al. (2013), we choose the liquidation boundary b=0.685, which means that the fund maximal loss that investors can tolerate is 31.5% of the HWM. As our assumption of the AUM P is similar to GIR, we take the same value of the fund's volatility as theirs that is calibrated from the data of 610 hedge funds, that is, σ = 15%. Further, the degree of the effort cost is set i=15, which insures that the range of the manager's effort is reasonable. To investigate the variation characteristics of the manager's optimal effort α (p) adequately, we set α a little higher, say, 0.1, to protect changes of α (p) from the impact of it.
4.1. Manager's optimal effort and value of total fees
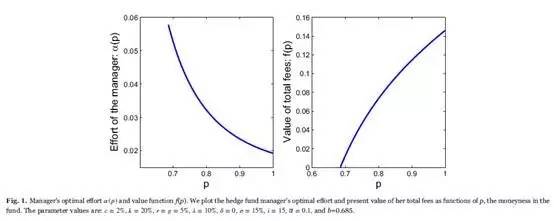
Fig. 1 plots the dynamic effort selected by the fund manager, which depends on the moneyness in the fund, p. At the liquidation boundary b=0.685, the manager's effort is at its highest level, α (b) = 0.0578. As p increases, the effort the manager makes decreases, and the rate of decline becomes slower. When p=1, α (1) declines to the lowest, 0.0192. The closer the fund is to liquidation, the greater effort the manager exerts, while the sooner the performance fee is to be paid, the more slowly the manager's effort declines.
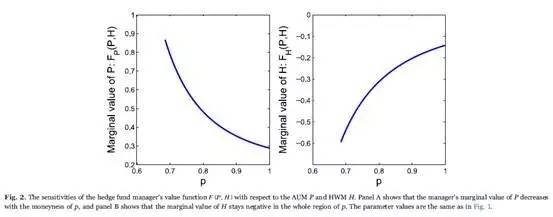
According to the homogeneity property, we have the sensitivities FP (P, H) = f ′(p) and FH (P, H) = f (p) ?pf ′(p), and the dynamics of the sensitivities are presented in Fig. 2. As p decreases from 1 to b=0.685, FP (P, H) increases from f ′(1) = 0.2884 to f ′(0.685) = 0.8672. When p is close to the lower boundary, the probability of liquidation rises and the marginal value of the value function with respect to P increases substantially. Because of the liquidation risk, a dollar increase of the AUM near the liquidation boundary is more valuable. In addition, the marginal value of H, FH (P, H), stays negative in the whole region, with the highest value FH (H, H) = f (1) ?f ′(1) = ?0.1423 when performance fees are to be paid, and the lowest value ?0.5940 at the liquidation boundary. The negative impact of an increasing H on the value function is significant, and an increase of H lowers the manager's value of total fees. Once the HWM H is crossed and reset, the long-term fund value is reduced and more close to the liquidation boundary due to the payoff of performance fees.
In our model, besides the high-water mark contracts, the manager also needs to consider the costly loss of all future fees upon liquidation. As shown before, an increase of the AUM near liquidation is worth more, that is, FP (P, H) is larger. In our model, the manager's effort α is directly proportional to FP (P, H), indicating that the manager tends to endeavor to increase the fund's AUM and reduce liquidation risk. So the optimal effort α (p) stays the highest at liquidation. Raising the effort given great effort cost can be viewed as a risk-averse managerial behavior. The manager has incentives to mitigate risks and pursue better future payoffs. On the other hand, when the fund is far from the danger of liquidation, i.e., the moneyness p is far away from b=0.685, the manager's effort declines quickly.
In addition, when the moneyness p gets closer to 1, that is, the AUM is close to the HWM, the manager's effort still declines, and the rate becomes slower. The unwillingness to bring the fund value to cross the HWM too soon can be explained by the following reasons. As the changes of FH (P, H) remind us, if a new higher H is reset, then future options to receive performance fees become more out of the money and the fund value's distance from the liquidation boundary reduces due to the payoff of performance fees. So a risk-neutral manager is averse to collect performance fees too soon, to maintain the value of both her compensation fees and the fund' AUM. Moreover, since greater effort takes more cost, the manager does not increase her effort after the trade-off between benefits and cost. However, due to the forthcoming performance fees, the rate of the effort decline is becoming slower.
In conclusion, from the perspective of the optimal effort, our model reflects the manager's risk-averse behavior near liquidation and unwillingness to prompt the fund's AUM to cross the HWM simultaneously. Given the high-water mark contracts and endogenous fund liquidation, when the fund value is either approaching liquidation or the high-water mark, the optimal effort chosen by the fund manager contributes to both maintaining the fund as a going concern and increasing the likelihood of survival for the fund, which are beneficial for the fund's survival and its investors. This incentive mechanism of hedge funds induces the manager to make efficient effort.
Our findings with respect to the optimal effort are contrast to those in a standard framework, such as Zhan (2011) and Ray and Chakraborty (2008). In the standard settings, there is no hypothesis of liquidation, especially endogenous liquidation, and the high-water mark contracts are the only factor to be considered. The high-water marks can be regarded as the strike prices of a series of call options on the fund's AUM. Once the strike price is crossed, the manager gains performance fees based on the excess profit of the AUM and then a new strike price is reset. It is natural that the manager exerts greater effort when the call option is about to be in the money. Our model assumptions can cover the standard settings, with no liquidation boundary (b = 0), and the result is shown in Section 4.2. In this case, we can see that the manager's effort indeed increases as the call option is closing to be in-the-money, i.e., as p is closing to 1, which agrees with the intuition behind the standard settings.
Specifically, Zhan (2011) realizes that the function of the HWM is double-fold. When the fund's AUM is close to its HWM, more effort will be induced; when the fund is too deep under the water and the manager's skill is too low to recover the loss, the efforts will be dampened. Ray and Chakraborty (2008) first define the required return to reach the HWM, which has positive correlation with the fund value's distance from the HWM. And they conclude that the optimal effort decreases as the required return to reach the HWM increases, that is, as the fund value's distance from the HWM increases. Moreover, they use realized excess returns as a proxy of the effort and run the regression of the returns on the required return to reach the HWM of previous month. It turns out that for funds whose required return is greater than 10%, the coefficient is negative but not significant, while for funds whose required return is less than 10%, the coefficient is significantly negative. The authors suggest that the empirical analysis can support their theoretical conclusion. However, utilizing realized excess returns as the proxy of the effort directly is quite questionable, since the effort is not the only factor to impact excess returns, and many other factors can explain excess returns as well. Their empirical results may also be explained by the following reasons. A good-skill manager could earn more excess returns, making the fund value more close to the HWM due to good performance, so the extra returns on funds whose value approaches the HWM are more likely to be higher. The results may have nothing to do with the manager's effort.
The reason that our findings regarding the effort are in contrast to theirs lies in our rational model specifications. In Zhan (2011), as well as Ray and Chakraborty (2008), the fund is not faced with liquidation during the single life period. However, in practice, investors tend to liquidate a fund even if the fund value falls a relatively small scale below the HWM. To protect themselves from large losses, the endogenous liquidation boundary b is usually close to 1. Our model assumption is more practical in that it incorporates both the HWM contracts and endogenous fund liquidation. By the comparison of the cases b=0.685 and b=0, we conclude that fund liquidation is one important risk that could determine the manager's choice of the effort. In Section 4.2, we will point out that the optimal effort deduced in the standard settings is not beneficial for funds's survival and its investors.
4.2. Special case with no liquidation boundary
With no liquidation boundary (b = 0), our model assumptions cover the standard settings mentioned before. The framework of the standard settings excludes the probability of endogenous liquidation, and only emphasizes on the HWM contracts.
As shown in Fig. 3, the optimal effort α is increasing as p increases, with a faster growth rate near p=1. In addition, the value function f(p) is convex due to the trend of the effort. The call option feature of the HWM contracts prompts the manager to make greater effort when the option is about to be in the money, that is, p is near 1. On the other hand, since the manager does not need to confront endogenous liquidation risk, the effort decreases as the fund's AUM is far from the HWM.
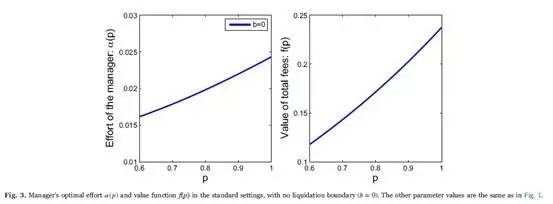
Greater effort near p=1 insures the manager receive performance fees soon, which harms the long-term growth of the fund's wealth due to the payoffs. Moreover, less effort, when the fund's value is shrinking, is averse to the recovery of the fund's AUM. In the standard settings, the chosen effort by the manager does not contribute to either increasing the likelihood of survival for the fund, or maintaining the fund's going-concern value. While in our model, the incentive mechanism deriving from both the high-water mark contracts and the endogenous liquidation induces efficient effort.
4.3. Deterministic case
When the manager's effort is chosen deterministically, α becomes a constant parameter, and the corresponding solution can be derived explicitly.
Under the assumption that the manager's effort α is determined, the value function f(p) satisfies the following ODE equation:
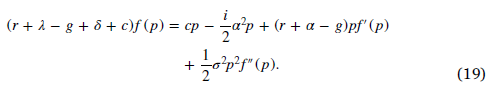
The boundary conditions of the equation are the same as Eq. (13),


4.4. Impacts of parameters referring to manager's personality and market conditions
The degree of the effort cost i is influenced by market conditions, such as the information value of target financial markets, the manager's opportunity costs of working elsewhere, as well as the manager's personality, which differs by individual. The AUM's return volatility σ in our paper is a constant parameter, indicating the extent of market fluctuations or certain leverage choice the manager adopts. In addition, the probability of exogenous liquidation λ, the investors' redemption rate δ and the liquidation boundary b are all investors' endogenous choices, depending on market conditions and the manager's performance. Specifically, λ and δ both stand for the investors' liquidity need, reflecting market sentiment or more profitable investment opportunities outside.
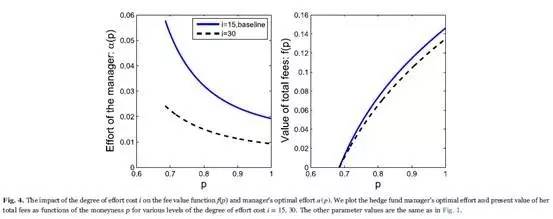
First, the degree of the effort cost i measures the expensiveness of the manager's endeavor. As in Fig. 4, the larger i gets, the less effort the manager makes, given higher effort cost. An increase in the degree of the effort cost from 15 to 30 decreases the optimal effort by about 50% both at the lower and upper boundaries, and α (p) decreases significantly among the whole range of the moneyness p. Although the value of total fees f(p) decreases as i increases, the change is slight. The reason is that lower effort has two effects on the value function, causing the AUM and thus the fees to be less valuable, and meanwhile resulting in less effort cost.
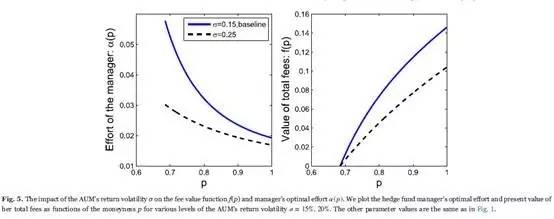
Second, an increase of the return volatility represents that the uncertainty of the fund's return, and further the AUM, increase. The uncertainty may stem from market fluctuations or leverage strategies. Hence, the fund manager's control of the fund is weakened and the motivation to endeavor is reduced. As in Fig. 5, the manager's optimal effort α (p) reduces when σ = 0.25, comparing to the situation of σ = 0.15. Specially, near the liquidation boundary, the probability of liquidation is larger when σ is higher, in spite of more effort, so the manager's optimal effort α (p) decreases substantially, from 0.0578 to 0.0302. Besides, although the manager has reduced her effort and thus her effort cost decreases, the value of total fees still shrinks observably. At p=1, the fee value decreases by around 30 percent.
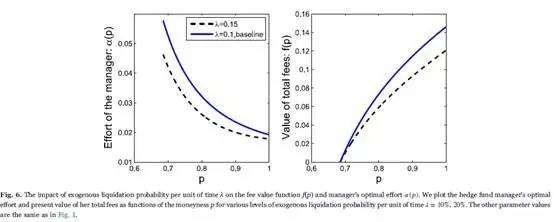
Third, a larger probability λ implies a greater likelihood of liquidation, while a larger redemption proportion δ decreases the AUM, and further, the total fees at a larger scale. Impacts of the probability of exogenous liquidation λ and the redemption rate δ are the same, so we only take one of the two into account. Larger λ weakens the manager's incentives to make effort, so α (p) shown in Fig. 6 declines. Since the impact of λ has nothing to do with the relative degree of p, the extent of the effort's decrease is similar across various levels of p.
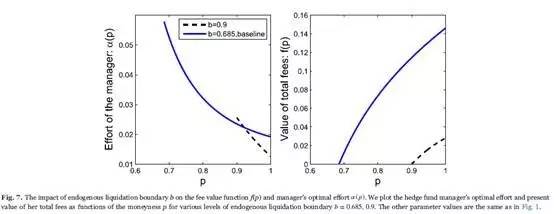
Finally, in China, to avoid massive losses, b=0.9 is common for hedge funds. In the case of b=0.9, the manager's optimal effort increases as p approaches this liquidation as well. A higher value of b increases the liquidation likelihood and hitting the boundary cancels all future payoffs. The manager suffers from more restrictions on investment strategies with a higher boundary level, thus the effort α (p) and the fee value f(p) both decreasing when the fund value is distant from the liquidation boundary, as depicted in Fig. 7. In particular, at p=1, an increase of b results in that the value of total fees decreases from 0.1461 to 0.0280, of which the distance is huge. Still, if b=0.9, the manager has incentives to exert herself at the liquidation boundary, so that the effort near p=0.9 exceeds the one with b=0.685.
4.5. Impacts of compensation contracts
The rates of management and performance fees, c and k, in the compensation contracts can be negotiated and adjusted. GIR discuss the trade-off between management fees and performance fees in detail. Here we investigate impacts of both fees on the manager's effort, total fee value of the manager and investors' value function.
Fig. 8 indicates that larger c results in greater effort α (p) in the whole range of p. Besides, the impacts of changing c from 0.02 to 0.03 and from 0.02 to 0.01 are not symmetric. The decline of c has more negative effects on α (p). Similarly, a larger k brings the manager richer rewards when the AUM crosses the HWM, and results in more effort. Comparing to the impact of the management fee rate c, near the HWM, the performance fee rate k has greater influences on the manager's effort. If more performance fees are to be paid, the effort α (p) will decrease more slowly near p=1. In addition, the impacts of changing k from 0.2 to 0.3 and from 0.2 to 0.1 are also not symmetric.
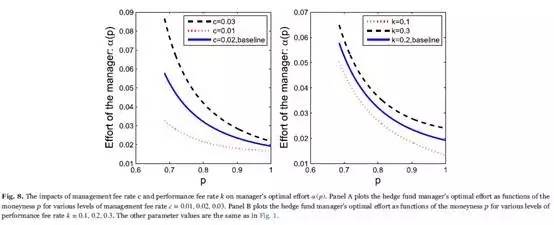
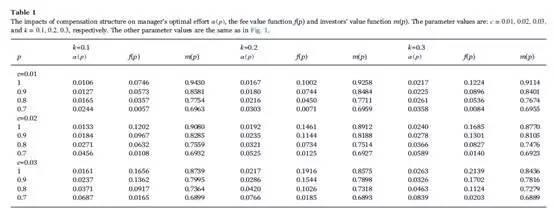
Table 1 reports the influences of variations of c and k on the manager's effort , value of total fees f(p) and investors' value m(p) in detail. First, as c and k increase, the manager's total fees f(p) become more valuable along all values of p intuitively. Especially, f(p) increases substantially near p=1 when the performance fee rate k increases. However, an increase of fee rates causes investors' value to shrink, since more fees are paid to the manager. Second, clearly, a decline of either c or k has greater impacts on all the three values (α, f and m) than an increase. For example, take and p=1 as a base case. An increase of k to 0.3 causes approximately a 21.2% increase of α, 11.6% increase of f and 1.6% decrease of m, while a decrease of k to 0.1 causes around 25.8% decease of α, 13.6% decease of f, and 1.9% increase of m. Finally, except the situation of p=1, the impact of c on the three values is stronger than that of k. It motivates more manager's effort, creates more compensation to the manager, and at the same time, takes away more investors' value. So from the perspective of the impacts, it can be concluded that management fees contribute to the compensation contracts more significantly.
4.6. Empirical results
We mainly need to discover the empirical relationship between the fund's distance from liquidation in the previous period and the riskadjusted extra returns α, to investigate whether liquidation risks induce more effort. Meanwhile, we should try to exclude the impacts of market opportunities, fund leverage, manager's skill and luck on risk-adjusted returns, to concentrate on the impact of manager's effort. Our study uses data from a database that contains the most comprehensive data of hedge funds in China and focuses on funds that specify a liquidation boundary in fund contracts.
Following Brown et al. (1999), we use the fund return in excess of the median return of funds applying the same strategy to measure riskadjusted returns, α. Besides, we define a ratio as the relative distance from liquidation, to represent the distance that the fund value is from liquidation. The ratio is calculated as the difference between the fund's share value and the liquidation boundary per share divided by the liquidation boundary per share.
During the same time period, the impact of market opportunities on hedge funds of the same strategy is almost the same. Therefore, we collect the cross-sectional data of risk-adjusted monthly returns in November, 2016, on the funds whose relative distance from liquidation was less than 20% in the previous month. In all 172 samples, the mean value of the liquidation boundary is 0.75, and more than 90% of the funds apply similar equity or futures strategies. Meanwhile, the calculation method of the risk-adjusted returns also excludes the returns that could be simply explained by market opportunities and reserves the returns that may be explained by the fund's unique characteristics to some extent, by subtracting the median return in the strategy to which the fund belongs from the fund return.
Statistically, we first classify the samples of fund returns into groups by the relative distance from liquidation, making sure that the sample sizes in each group are similar. The intervals of the relative distance from liquidation in the previous month of each group are [0, 5%), [5%, 10%), [10%, 15%), and [15%, 20%). The intervals for classification, mean risk-adjusted returns and standard deviations in each group are show in Table 2.
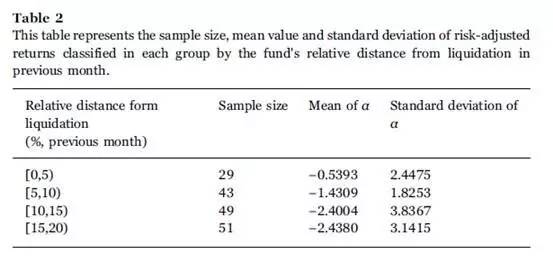
From Table 2, we can see that the mean values of risk-adjusted returns in the group in which the fund's relative distance from liquidation belongs to the range [0, 5%), [5%, 10%), and [10%, 15%) decrease gradually, but the mean values in the groups of [10%, 15%) and [15%, 20%) are almost equal. Further, we apply Welch's t-test to test whether the means between two adjacent groups are significantly different, and the test is usually used when the two sample sizes are not equal and the two population variances are not assumed to be equal. The hypothesis is one sided and the corresponding t-statistics is calculated as follows,

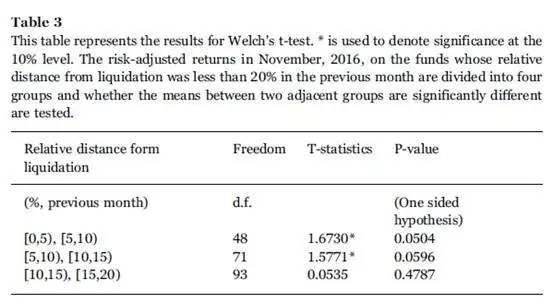
The results of Welch's t-test are displayed on Table 3. We find that the mean risk-adjusted return on funds whose relative distance from liquidation lies in the range of [0, 5%) is higher than that in [5%, 10%) at 10% level of significance, and so is the case with the groups of [5%, 10%) and [10%, 15%). However, when comparing with the groups of [10%, 15%) and [15%, 20%), the disparity is not significant. Given the results, we may conclude that the manager's effort is an important factor to explain a fund's extra return, especially when the fund is approaching liquidation. When the fund is sufficiently close to liquidation, the manager tends to exert greatest effort, to increase the likelihood of survival for the fund and preserve the fund's goingconcern value.
To make the empirical results more rigorous, we still need to discuss whether the impacts of the manager's skill, luck and leverage choice on extra returns can also explain our empirical findings. First, the impacts of skill can be excluded. Generally, the performance of funds governed by high-skill managers is more likely better and away from liquidation. It is reasonable to conjecture that the skill of the fund managers who govern funds that are more close to liquidation is always lower, and the returns on these funds are lower, which is contrast to our empirical findings. Next, the impacts of luck can also be excluded easily, since there is no evidence that the poor performance of a fund induces better luck. Most importantly, the effects of leverage should be considered prudently. In China, the fund with a specified liquidation boundary usually has another boundary named warning line, and the warning line per share is usually set 5% higher than the liquidation boundary. When the fund share value falls below the warning line per share, the manager needs to decrease the fund leverage, that is, decrease the assets allocated in the investment strategy and increase the amount of cash assets. If extra returns of the investment strategy developed by a low-skill manager are negative, reducing the positions in the strategy can somewhat lead to an increase of returns. So our empirical results may derive from the de-leverage of low-skill manager when the fund is sufficiently close to liquidation. To mitigate the possible impacts of leverage on the results, we further pick up the samples of funds whose share value is above the warning line so that the action of de-leverage is not triggered, from the previous samples. In the new samples, the sample size of the group of [0, 5%) is much smaller, which is not suitable to the testing. The disparity between the mean risk-adjusted returns on funds whose relative distance from liquidation lies in the range of [5%, 10%) and [10%, 15%) is still significant at the 10% level. The sample size of them are 31 and 44, the mean values are ?1.5739 and ?2.4334, and the standard deviations are 3.4408 and 14.3008, respectively. The P-value of the t-statistics is 0.0987, slightly higher than the previous P-value, 0.0596.
In conclusion, after trying to exclude the potential impacts of other factors, such as market opportunities, manager's skill, luck and leverage, we may confirm that higher extra returns on funds that are sufficiently close to liquidation are due to higher effort of managers. Our theoretical research can give a direction for empirical analysis and facilitate future research.
5.Conclusion
We utilize the extra return of the fund's AUM as a control variable to measure the manager's optimal effort, and the manager can choose the optimal effort to maximize the value of her total fees and reduce liquidation risks. Specifically, we extend the log-normal diffusion process of the AUM in GIR, with an extra return α to be determined. The risk-neutral hedge fund manager needs to make the trade-off between the benefits of extra returns and the quadratic cost of the effort. We find that the manager's effort relies on the fund's AUM distance from its HWM.
The closer the fund is to liquidation, the greater effort the manager chooses to make, and when liquidation is immediate, the manager tends to exert greatest effort. This is non-intuitive at first and opposite to the intuition of standard settings. In our model, besides the special high-water mark contracts, the manager also has to consider the loss of all future payoffs once the downside liquidation occurs. So she has the incentive to reduce this risk and behaves risk-averse. Moreover, when the fund's AUM approaches the HWM, the manager's optimal effort still decreases, implying that a risk-neutral manager is reluctant to see the fund cross the HWM too soon, since the payoff of performance fees reduces long-term asset growth. In summary, we find that endogenous liquidation plays a key role in the selection of the effort, and given the high-water mark contracts, as well as the endogenous liquidation, when the fund value is either approaching liquidation or the high-water mark, the optimal effort contributes to helping the survival of the fund and preserving the fund's going-concern value.
Moreover, the manager's optimal effort decreases with the degree of the effort cost, volatility of the AUM, exogenous liquidation probability or endogenous liquidation boundary. Higher rate of management fees or performance fees induces a higher effort, more total fees paid to the manager and a lower level of investors' wealth. All these three values are more sensitive to a decline of either management or performance fees than an increase. Management fees play a major role in influencing the manager's effort, and both the manager's and investor's value functions.
Our theoretical conclusion may be supported by the empirical evidence derived from hedge funds in China. It is a pity that a suitable proxy variable of the manager's effort is difficult to be determined, and this can be future topics in the empirical research on funds' performance.


(完)
